Release new version
Features:
- Particle systems can now specify a maximum dt per step
- Animation key-framing & timing system now supports objects with simulation
- Mixture/multiple importance sampling for correct low-variance direct lighting
- New BSDF, point light, and environment light APIs that separate sampling, evaluation, and pdf
- Area light sampling infrastructure
- Removed rectangle area lights; all area lights are now emissive meshes
- Reworked PathTracer tasks 4-6, adjusted/improved instructions for the other tasks
Bug fixes:
- Use full rgb/srgb conversion equation instead of approximation
- Material albedo now specified in srgb (matching the displayed color)
- ImGui input fields becoming inactive no longer apply to a newly selected object
- Rendering animations with path tracing correctly steps simulations each frame
- Rasterization based renderer no longer inherits projection matrix from window
- Scene file format no longer corrupts particle emitter enable states
- Documentation videos no longer autoplay
- Misc. refactoring
- Misc. documentation website improvements
Showing
- docs/pathtracer/dielectrics_and_transmission.md 0 additions, 33 deletionsdocs/pathtracer/dielectrics_and_transmission.md
- docs/pathtracer/direct_lighting.md 77 additions, 0 deletionsdocs/pathtracer/direct_lighting.md
- docs/pathtracer/environment_lighting.md 54 additions, 32 deletionsdocs/pathtracer/environment_lighting.md
- docs/pathtracer/envmap_gui.png 0 additions, 0 deletionsdocs/pathtracer/envmap_gui.png
- docs/pathtracer/figures/BVH_construction_pseudocode.png 0 additions, 0 deletionsdocs/pathtracer/figures/BVH_construction_pseudocode.png
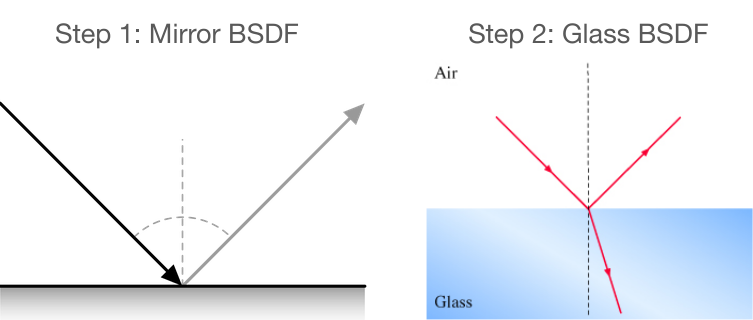
- docs/pathtracer/figures/bsdf_diagrams.png 0 additions, 0 deletionsdocs/pathtracer/figures/bsdf_diagrams.png
- docs/pathtracer/figures/dielectric_eq1.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq1.png
- docs/pathtracer/figures/dielectric_eq10.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq10.png
- docs/pathtracer/figures/dielectric_eq2.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq2.png
- docs/pathtracer/figures/dielectric_eq3.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq3.png
- docs/pathtracer/figures/dielectric_eq4.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq4.png
- docs/pathtracer/figures/dielectric_eq5.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq5.png
- docs/pathtracer/figures/dielectric_eq6.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq6.png
- docs/pathtracer/figures/dielectric_eq7.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq7.png
- docs/pathtracer/figures/dielectric_eq8.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq8.png
- docs/pathtracer/figures/dielectric_eq9.png 0 additions, 0 deletionsdocs/pathtracer/figures/dielectric_eq9.png
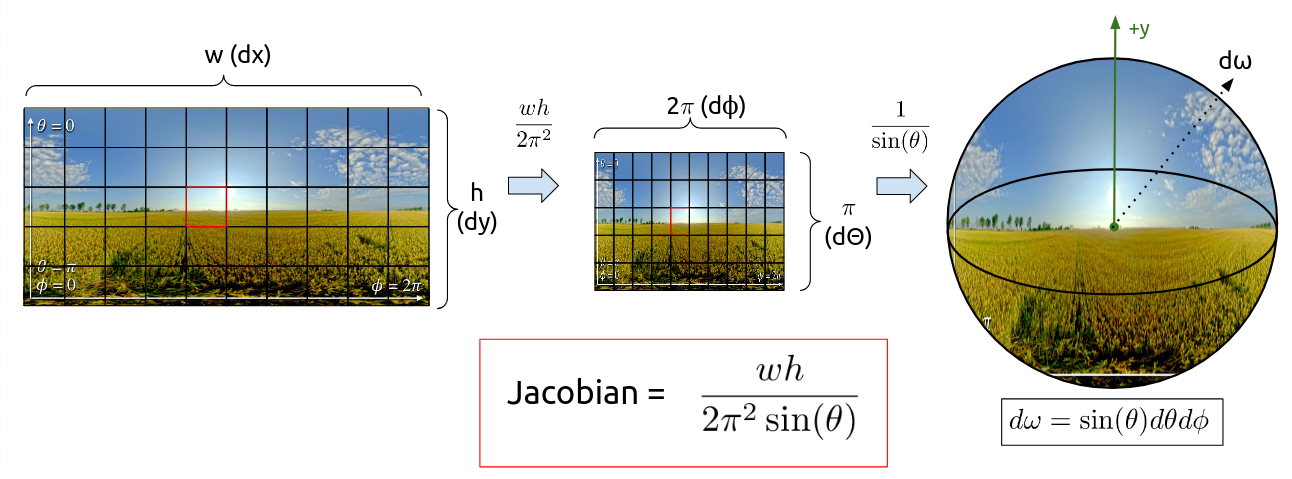
- docs/pathtracer/figures/env_light_sampling_jacobian_diagram.png 0 additions, 0 deletions...athtracer/figures/env_light_sampling_jacobian_diagram.png
- docs/pathtracer/figures/environment_eq1.png 0 additions, 0 deletionsdocs/pathtracer/figures/environment_eq1.png
- docs/pathtracer/figures/environment_eq10.png 0 additions, 0 deletionsdocs/pathtracer/figures/environment_eq10.png
- docs/pathtracer/figures/environment_eq11.png 0 additions, 0 deletionsdocs/pathtracer/figures/environment_eq11.png
docs/pathtracer/direct_lighting.md
0 → 100644
docs/pathtracer/envmap_gui.png
deleted
100644 → 0
483 KiB
File moved
docs/pathtracer/figures/bsdf_diagrams.png
0 → 100644
65.1 KiB
File moved
515 KiB
File moved
File moved
File moved