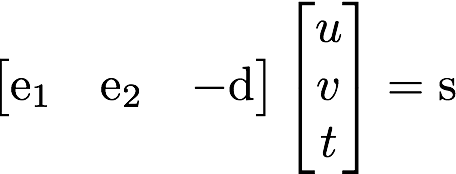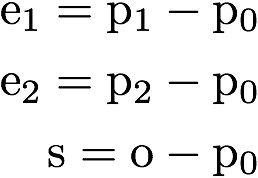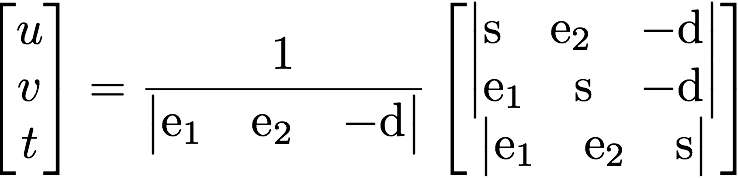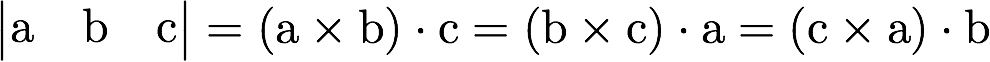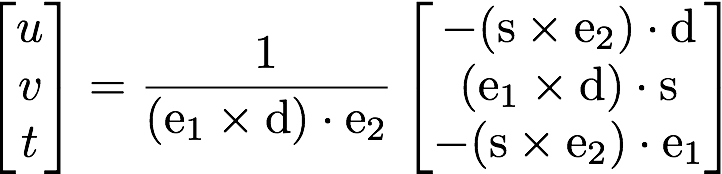pathtracer doc 1st draft
Showing
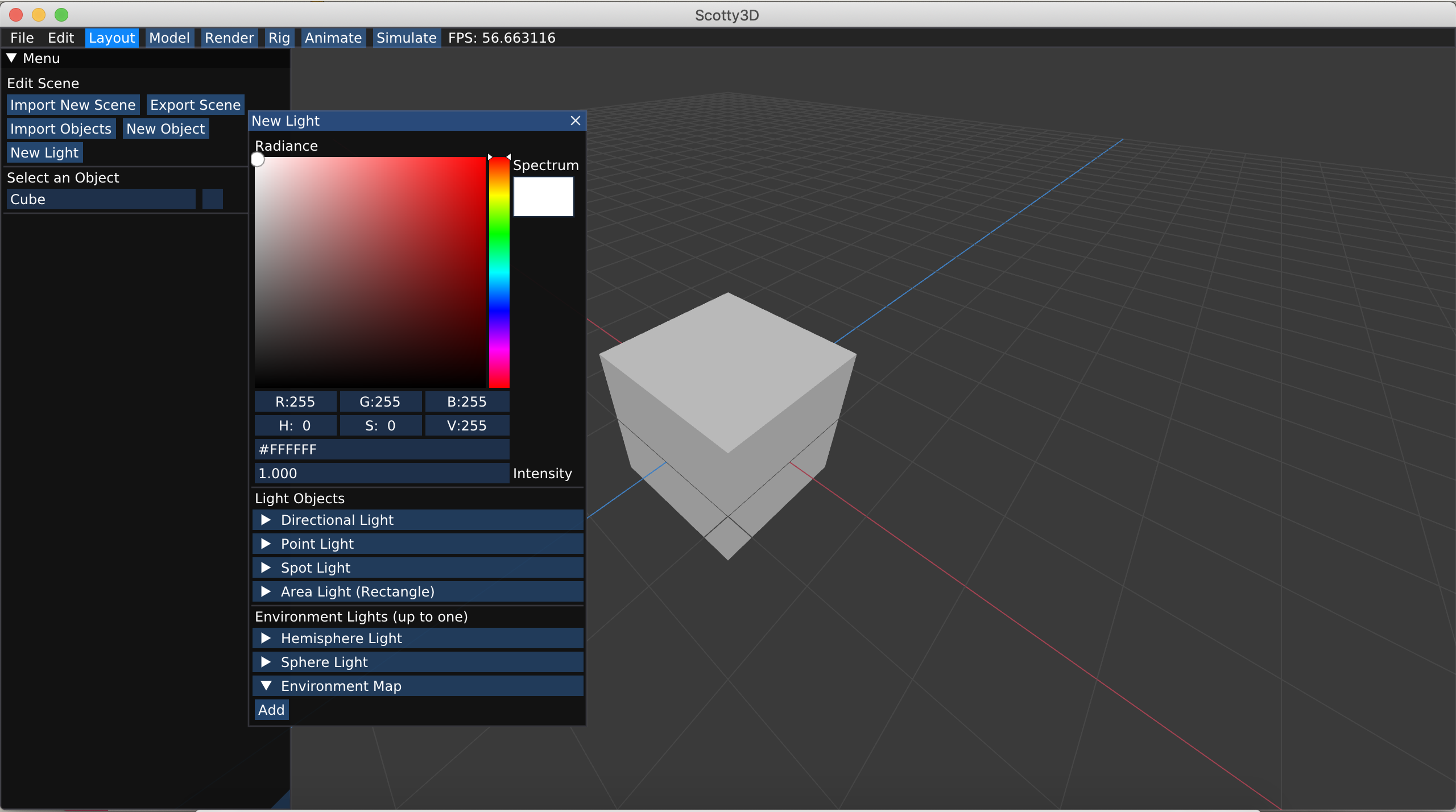
- docs/pathtracer/envmap_gui.png 0 additions, 0 deletionsdocs/pathtracer/envmap_gui.png
- docs/pathtracer/importance_sampling.md 22 additions, 0 deletionsdocs/pathtracer/importance_sampling.md
- docs/pathtracer/intersecting_objects.md 53 additions, 0 deletionsdocs/pathtracer/intersecting_objects.md
- docs/pathtracer/materials.md 41 additions, 0 deletionsdocs/pathtracer/materials.md
- docs/pathtracer/normalviz.png 0 additions, 0 deletionsdocs/pathtracer/normalviz.png
- docs/pathtracer/overview.md 27 additions, 0 deletionsdocs/pathtracer/overview.md
- docs/pathtracer/path_tracing.md 49 additions, 0 deletionsdocs/pathtracer/path_tracing.md
- docs/pathtracer/ray_triangle_intersection.md 30 additions, 0 deletionsdocs/pathtracer/ray_triangle_intersection.md
- docs/pathtracer/rays_dir.png 0 additions, 0 deletionsdocs/pathtracer/rays_dir.png
- docs/pathtracer/shadow_directional.png 0 additions, 0 deletionsdocs/pathtracer/shadow_directional.png
- docs/pathtracer/shadow_hemisphere.png 0 additions, 0 deletionsdocs/pathtracer/shadow_hemisphere.png
- docs/pathtracer/shadow_rays.md 32 additions, 0 deletionsdocs/pathtracer/shadow_rays.md
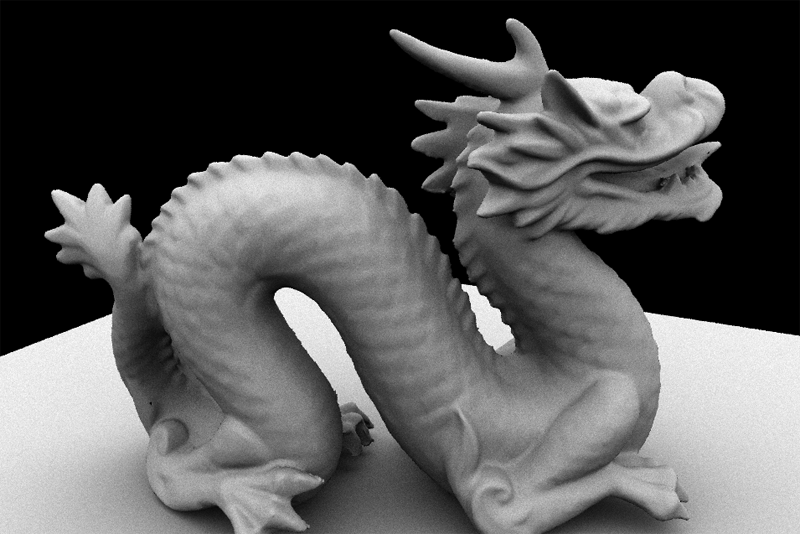
- docs/pathtracer/spheres.png 0 additions, 0 deletionsdocs/pathtracer/spheres.png
- docs/pathtracer/triangle_eq1.png 0 additions, 0 deletionsdocs/pathtracer/triangle_eq1.png
- docs/pathtracer/triangle_eq2.png 0 additions, 0 deletionsdocs/pathtracer/triangle_eq2.png
- docs/pathtracer/triangle_eq3.png 0 additions, 0 deletionsdocs/pathtracer/triangle_eq3.png
- docs/pathtracer/triangle_eq4.png 0 additions, 0 deletionsdocs/pathtracer/triangle_eq4.png
- docs/pathtracer/triangle_eq5.png 0 additions, 0 deletionsdocs/pathtracer/triangle_eq5.png
- docs/pathtracer/visualization_of_normals.md 20 additions, 0 deletionsdocs/pathtracer/visualization_of_normals.md
docs/pathtracer/envmap_gui.png
0 → 100644
483 KiB
docs/pathtracer/importance_sampling.md
0 → 100644
docs/pathtracer/intersecting_objects.md
0 → 100644
docs/pathtracer/materials.md
0 → 100644
docs/pathtracer/normalviz.png
0 → 100644
534 KiB
docs/pathtracer/overview.md
0 → 100644
docs/pathtracer/path_tracing.md
0 → 100644
docs/pathtracer/ray_triangle_intersection.md
0 → 100644
docs/pathtracer/rays_dir.png
0 → 100644
34.3 KiB
docs/pathtracer/shadow_directional.png
0 → 100644
148 KiB
docs/pathtracer/shadow_hemisphere.png
0 → 100644
289 KiB
docs/pathtracer/shadow_rays.md
0 → 100644
docs/pathtracer/spheres.png
0 → 100644
1.77 MiB
docs/pathtracer/triangle_eq1.png
0 → 100644
8.29 KiB
docs/pathtracer/triangle_eq2.png
0 → 100644
8.01 KiB
docs/pathtracer/triangle_eq3.png
0 → 100644
14.6 KiB
docs/pathtracer/triangle_eq4.png
0 → 100644
8.46 KiB
docs/pathtracer/triangle_eq5.png
0 → 100644
18.3 KiB
docs/pathtracer/visualization_of_normals.md
0 → 100644