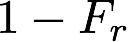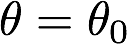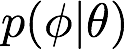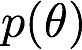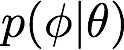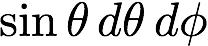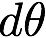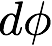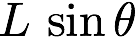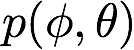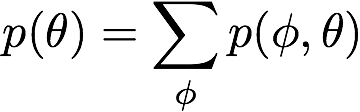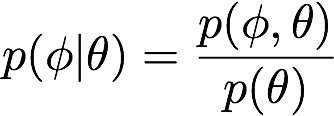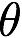pathtracer doc 1st draft
Showing
- docs/pathtracer/dielectric_eq5.png 0 additions, 0 deletionsdocs/pathtracer/dielectric_eq5.png
- docs/pathtracer/dielectric_eq6.png 0 additions, 0 deletionsdocs/pathtracer/dielectric_eq6.png
- docs/pathtracer/dielectric_eq7.png 0 additions, 0 deletionsdocs/pathtracer/dielectric_eq7.png
- docs/pathtracer/dielectric_eq8.png 0 additions, 0 deletionsdocs/pathtracer/dielectric_eq8.png
- docs/pathtracer/dielectric_eq9.png 0 additions, 0 deletionsdocs/pathtracer/dielectric_eq9.png
- docs/pathtracer/dielectrics_and_transmission.md 31 additions, 0 deletionsdocs/pathtracer/dielectrics_and_transmission.md
- docs/pathtracer/environment_eq1.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq1.png
- docs/pathtracer/environment_eq10.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq10.png
- docs/pathtracer/environment_eq11.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq11.png
- docs/pathtracer/environment_eq12.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq12.png
- docs/pathtracer/environment_eq2.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq2.png
- docs/pathtracer/environment_eq3.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq3.png
- docs/pathtracer/environment_eq4.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq4.png
- docs/pathtracer/environment_eq5.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq5.png
- docs/pathtracer/environment_eq6.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq6.png
- docs/pathtracer/environment_eq7.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq7.png
- docs/pathtracer/environment_eq8.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq8.png
- docs/pathtracer/environment_eq9.png 0 additions, 0 deletionsdocs/pathtracer/environment_eq9.png
- docs/pathtracer/environment_lighting.md 44 additions, 0 deletionsdocs/pathtracer/environment_lighting.md
- docs/pathtracer/envmap_figure.jpg 0 additions, 0 deletionsdocs/pathtracer/envmap_figure.jpg
docs/pathtracer/dielectric_eq5.png
0 → 100644
6.25 KiB
docs/pathtracer/dielectric_eq6.png
0 → 100644
10.3 KiB
docs/pathtracer/dielectric_eq7.png
0 → 100644
10.3 KiB
docs/pathtracer/dielectric_eq8.png
0 → 100644
2.64 KiB
docs/pathtracer/dielectric_eq9.png
0 → 100644
3 KiB
docs/pathtracer/environment_eq1.png
0 → 100644
3.19 KiB
docs/pathtracer/environment_eq10.png
0 → 100644
4.36 KiB
docs/pathtracer/environment_eq11.png
0 → 100644
3.56 KiB
docs/pathtracer/environment_eq12.png
0 → 100644
4.36 KiB
docs/pathtracer/environment_eq2.png
0 → 100644
4.86 KiB
docs/pathtracer/environment_eq3.png
0 → 100644
2.89 KiB
docs/pathtracer/environment_eq4.png
0 → 100644
2.97 KiB
docs/pathtracer/environment_eq5.png
0 → 100644
3.73 KiB
docs/pathtracer/environment_eq6.png
0 → 100644
4.27 KiB
docs/pathtracer/environment_eq7.png
0 → 100644
7.29 KiB
docs/pathtracer/environment_eq8.png
0 → 100644
9.31 KiB
docs/pathtracer/environment_eq9.png
0 → 100644
2.43 KiB
docs/pathtracer/environment_lighting.md
0 → 100644
docs/pathtracer/envmap_figure.jpg
0 → 100644
130 KiB