new docs dump
Showing
- docs/meshedit/global/simplify/plane_normal.png 0 additions, 0 deletionsdocs/meshedit/global/simplify/plane_normal.png
- docs/meshedit/global/simplify/quad_example.png 0 additions, 0 deletionsdocs/meshedit/global/simplify/quad_example.png
- docs/meshedit/global/simplify/quad_simplify.png 0 additions, 0 deletionsdocs/meshedit/global/simplify/quad_simplify.png
- docs/meshedit/global/simplify/vert_normals.png 0 additions, 0 deletionsdocs/meshedit/global/simplify/vert_normals.png
- docs/meshedit/global/triangulate/triangulate.png 0 additions, 0 deletionsdocs/meshedit/global/triangulate/triangulate.png
- docs/meshedit/halfedge.md 7 additions, 5 deletionsdocs/meshedit/halfedge.md
- docs/meshedit/linear.md 6 additions, 4 deletionsdocs/meshedit/linear.md
- docs/meshedit/local.md 8 additions, 4 deletionsdocs/meshedit/local.md
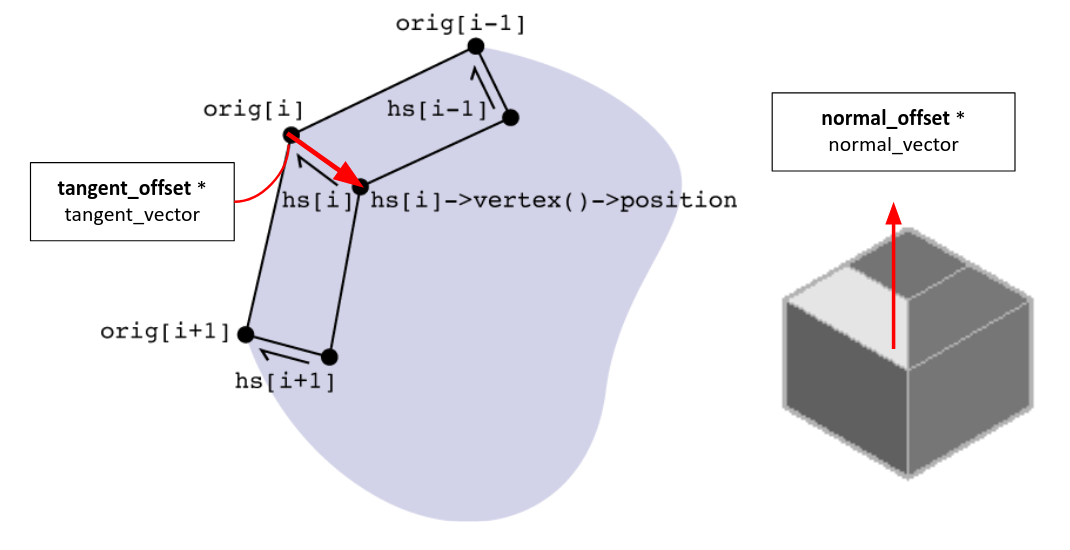
- docs/meshedit/local/bevel/bevel_diagram.png 0 additions, 0 deletionsdocs/meshedit/local/bevel/bevel_diagram.png
- docs/meshedit/local/bevel/bevel_indexing.png 0 additions, 0 deletionsdocs/meshedit/local/bevel/bevel_indexing.png
- docs/meshedit/local/bevel_edge.svg 0 additions, 0 deletionsdocs/meshedit/local/bevel_edge.svg
- docs/meshedit/local/bevel_face.svg 0 additions, 0 deletionsdocs/meshedit/local/bevel_face.svg
- docs/meshedit/local/bevel_vertex.svg 0 additions, 0 deletionsdocs/meshedit/local/bevel_vertex.svg
- docs/meshedit/local/collapse_edge.svg 0 additions, 0 deletionsdocs/meshedit/local/collapse_edge.svg
- docs/meshedit/local/collapse_face.svg 0 additions, 0 deletionsdocs/meshedit/local/collapse_face.svg
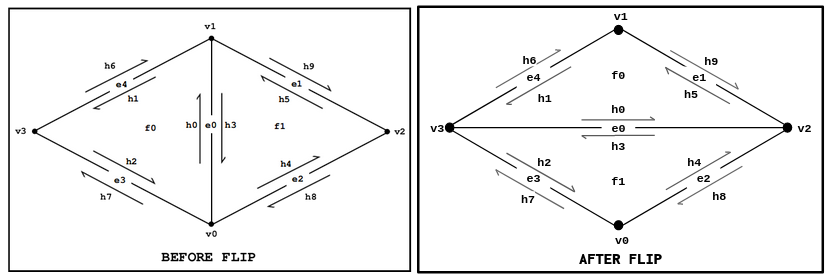
- docs/meshedit/local/edge_flip_diagram.png 0 additions, 0 deletionsdocs/meshedit/local/edge_flip_diagram.png
- docs/meshedit/local/erase_edge.svg 0 additions, 0 deletionsdocs/meshedit/local/erase_edge.svg
- docs/meshedit/local/erase_vertex.svg 0 additions, 0 deletionsdocs/meshedit/local/erase_vertex.svg
- docs/meshedit/local/flip_edge.svg 0 additions, 0 deletionsdocs/meshedit/local/flip_edge.svg
- docs/meshedit/local/split_edge.svg 0 additions, 0 deletionsdocs/meshedit/local/split_edge.svg
File moved
docs/meshedit/local/bevel/bevel_diagram.png
0 → 100644
86.6 KiB
File moved
File moved
File moved
File moved
File moved
docs/meshedit/local/edge_flip_diagram.png
0 → 100644
57.7 KiB
File moved
File moved
File moved
File moved