(Task 6) Materials

Now that you have implemented the ability to sample more complex light paths, it’s finally time to add support for more types of materials (other than the fully Lambertian material that you have implemented in Task 5). In this task you will add support for two types of materials: a perfect mirror and glass (a material featuring both specular reflection and transmittance) in student/bsdf.cpp.
To get started take a look at the BSDF interface in rays/bsdf.h. There are a number of key methods you should understand in BSDF class:
Spectrum evaluate(Vec3 out_dir, Vec3 in_dir): evaluates the distribution function for a given pair of directions.BSDF_Sample sample(Vec3 out_dir): given theout_dir, generates a random sample of the in-direction (which may be a reflection direction or a refracted transmitted light direction). It returns aBSDF_Sample, which contains the in-direction(direction), its probability (pdf), as well as theattenuationfor this pair of directions. (You do not need to worry about theemissivefor the materials that we are asking you to implement, since those materials do not emit light.)
There are also two helper functions in the BSDF class in student/bsdf.cpp that you will need to implement:
-
Vec3 reflect(Vec3 dir)returns a direction that is the perfect specular reflection direction corresponding todir(reflection ofdirabout the normal, which in the surface coordinate space is [0,1,0]). More detail about specular reflection is here. -
Vec3 refract(Vec3 out_dir, float index_of_refraction, bool& was_internal)returns the ray that results from refracting the ray inout_dirabout the surface according to Snell’s Law. The surface’s index of refraction is given by the argumentindex_of_refraction. Your implementation should assume that if the ray inout_diris entering the surface (that is, ifcos(out_dir, N=[0,1,0]) > 0) then the ray is currently in vacuum (index of refraction = 1.0). Ifcos(out_dir, N=[0,1,0]) < 0then your code should assume the ray is leaving the surface and entering vacuum. In the case of total internal reflection, you should set*was_internaltotrue. -
Note that in
reflectandrefract, both theout_dirand the returned in-direction are pointing away from the intersection point of the ray and the surface, as illustrated in this picture below.

Step 1
Implement the class BSDF_Mirror which represents a material with perfect specular reflection (a perfect mirror). You should Implement BSDF_Mirror::sample, BSDF_Mirror::evaluate, and reflect. (Hint: what should the pdf sampled by BSDF_Mirror::sample be? What should the reflectance function BSDF_Mirror::evalute be?)
Step 2
Implement the class BSDF_Glass which is a glass-like material that both reflects light and transmit light. As discussed in class the fraction of light that is reflected and transmitted through glass is given by the dielectric Fresnel equations.
Specifically your implementation should:
- Implement
refractto add support for refracted ray paths. - Implement
BSDF_refract::sampleas well asBSDF_Glass::sample. Your implementation should use the Fresnel equations to compute the fraction of reflected light and the fraction of transmitted light. The returned ray sample should be either a reflection ray or a refracted ray, with the probability of which type of ray to use for the current path proportional to the Fresnel reflectance. (e.g., If the Fresnel reflectance is 0.9, then you should generate a reflection ray 90% of the time. What should the pdf be in this case?) Note that you can also use Schlick’s approximation instead. - You should read the notes below on the Fresnel equations as well as on how to compute a transmittance BSDF.
Dielectrics and Transmission
Fresnel Equations for Dielectric
The Fresnel Equations (another link here) describe the amount of reflection from a surface. The description below is an approximation for dielectric materials (materials that don’t conduct electricity). In this assignment you’re asked to implement a glass material, which is a dielectric.
In the description below, ![]() and
and ![]() refer to the index of refraction of the medium containing an incoming ray, and the zenith angle of the ray to the surface of a new medium.
refer to the index of refraction of the medium containing an incoming ray, and the zenith angle of the ray to the surface of a new medium. ![]() and
and ![]() refer to the index of refraction of the new medium and the angle to the surface normal of a transmitted ray.
refer to the index of refraction of the new medium and the angle to the surface normal of a transmitted ray.
The Fresnel equations state that reflection from a surface is a function of the surface’s index of refraction, as well as the polarity of the incoming light. Since our renderer doesn’t account for polarity, we’ll apply a common approximation of averaging the reflectance of polarizes light in perpendicular and parallel polarized light:
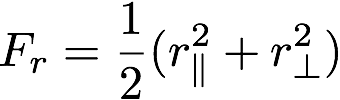
The parallel and perpendicular terms are given by:
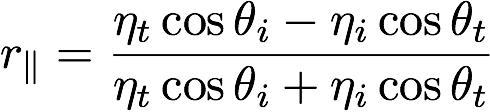
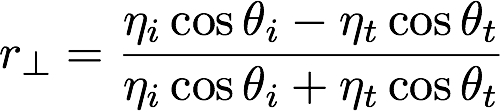
Therefore, for a dielectric material, the fraction of reflected light will be given by ![]() , and the amount of transmitted light will be given by
, and the amount of transmitted light will be given by 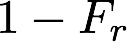 .
.
Alternatively, you may compute ![]() using Schlick’s approximation.
using Schlick’s approximation.
Distribution Function for Transmitted Light
We described the BRDF for perfect specular reflection in class, however we did not discuss the distribution function for transmitted light. Since refraction “spreads” or “condenses” a beam, unlike perfect reflection, the radiance along the ray changes due to a refraction event. In your assignment you should use Snell’s Law to compute the direction of refraction rays, and use the following distribution function to compute the radiance of transmitted rays. We refer you guys to Pharr, Jakob, and and Humphries’s book Physically Based Rendering for a derivation based on Snell’s Law and the relation 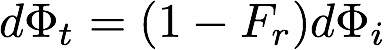 . (But you are more than welcome to attempt a derivation on your own!)
. (But you are more than welcome to attempt a derivation on your own!)
When you are done, you will be able to render images like these:
