add data and site info
1.54 MB
15.6 KB
13.8 KB
14.7 KB
8.7 KB
5.59 KB
7.25 KB
39.1 KB
928 KB
705 KB
211 KB
331 KB
63.7 KB
86.6 KB

1.54 MB

15.6 KB

13.8 KB
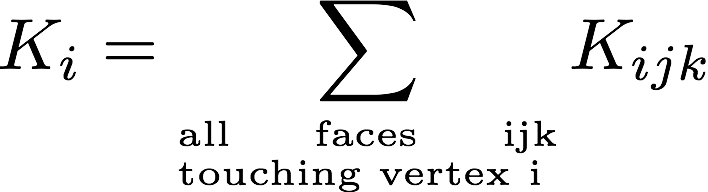
14.7 KB
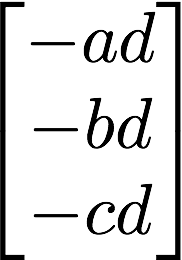
8.7 KB

5.59 KB

7.25 KB

39.1 KB

928 KB

705 KB

211 KB
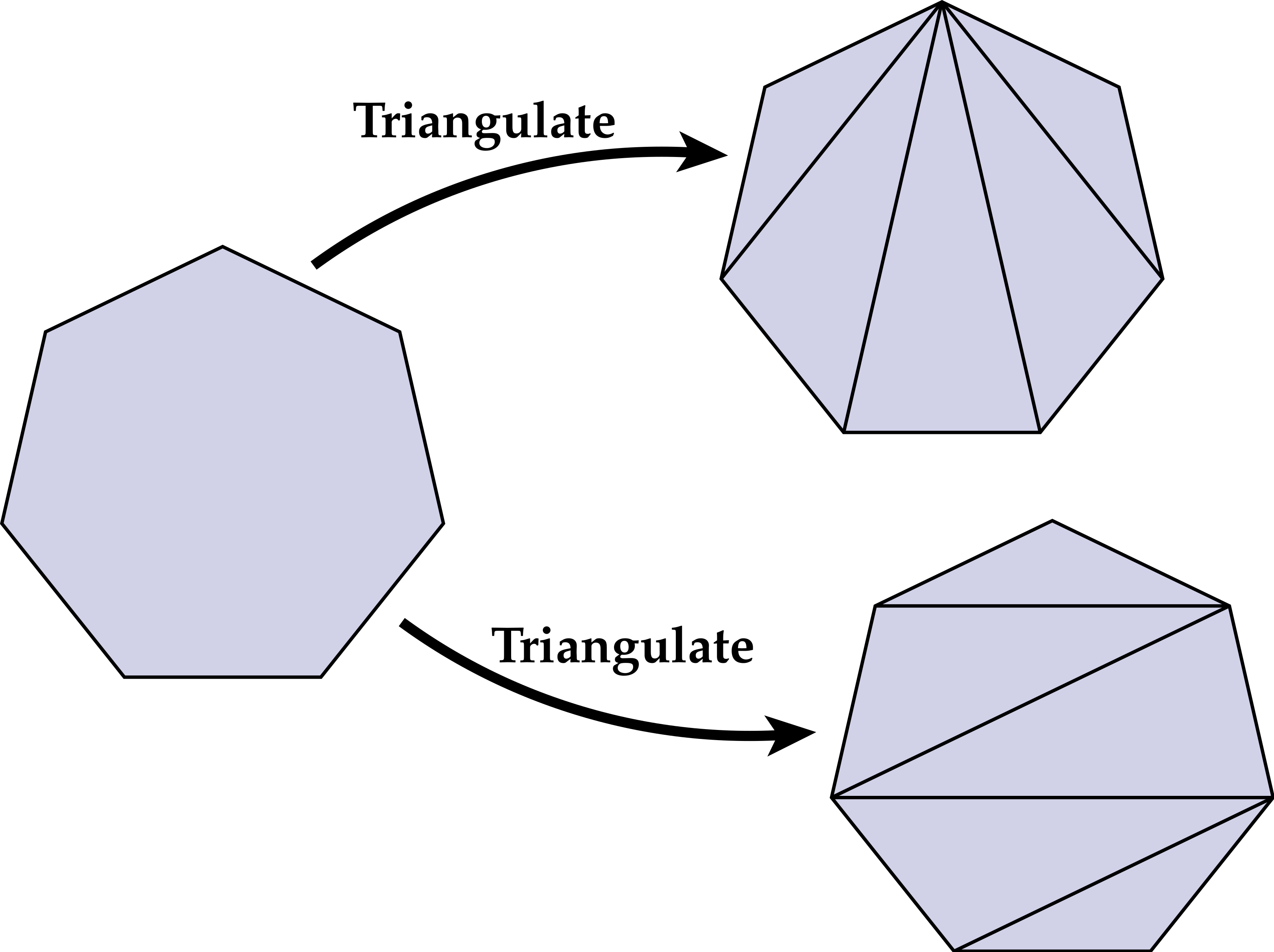
331 KB
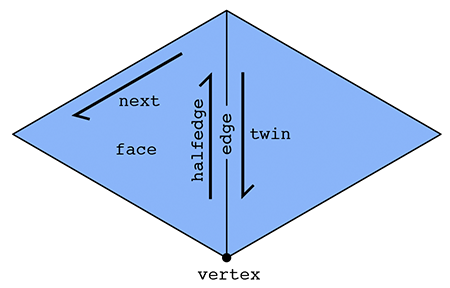
63.7 KB
86.6 KB